gerbang logika
RANGKAIAN LOGIKA (GERBANG LOGIKA)
(GERBANG LOGIKA)
Aplikasi Aljabar Boolean
1. Jaringan Pensaklaran (Switching Network)
Saklar merupakan objek yang mempunyai dua buah keadaan: buka dan tutup.
Tiga bentuk gerbang paling sederhana:
1.
2. keluaran b hanya ada jika dan hanya jika saklarx dibuka menuju x
3. keluaran b hanya ada jika dan hanya jika x dan y keduanya ditutup ke arah xy
keluaran c hanya ada jika dan hanya jika x atau y ditutup ke arah x + y
Contoh rangkaian pensaklaran pada rangkaian listrik:
Rangkaian pensaklaran pada rangkaian listrik dalam hubungan seri A dan B adalah saklar yang terpasang secara serial. Lampu hanya menyala jika A dan B ditutup. Dalam ekspresi Boolean ,hubungan serial ini dinyatakan sebagai AB. Sedangkan rangkaian pensaklran pada rangkaian listrik dalam hubungan pararel A dan B adalah saklar yang terpasang secara pararel.Lampu hanya menyala jika salah satu dari A dan B ditutup. Dalam ekspresi Boolean , hubungan pararel ini dinyatakan sebagai A + B.
Contohnya Nyatakan rangkaian pensaklaran pada gambar di bawah ini dalam ekspresi Boolean.
Jawab: x’y + (x’ + xy)z + x(y + y’z + z)
2. Rangkaian Digital Elektronik
Contoh.
Nyatakan fungsi f(x, y, z) = xy + x’y ke dalam rangkaian logika.
Jawab: (a) Cara pertama
(b) Cara kedua
(b) Cara ketiga
Gerbang turunan
Penyederhanaan Fungsi Boolean
Contoh. f(x, y) = x’y + xy’ + y’
disederhanakan menjadi
f(x, y) = x’ + y’
Penyederhanaan fungsi Boolean dapat dilakukan dengan 3 cara:
1. Secara aljabar
2. Menggunakan Peta Karnaugh
3. Menggunakan metode Quine Mc Cluskey (metode Tabulasi)
1. Penyederhanaan Secara Aljabar
Contoh:
1. f(x, y) = x + x’y
= (x + x’)(x + y)
= 1 × (x + y )
= x + y
2. f(x, y, z) = x’y’z + x’yz + xy’
= x’z(y’ + y) + xy’
= x’z + xz’
3. f(x, y, z) = xy + x’z + yz = xy + x’z + yz(x + x’)
= xy + x’z + xyz + x’yz
= xy(1 + z) + x’z(1 + y) = xy + x’z
2. Peta Karnaugh
a. Peta Karnaugh dengan dua peubah
y
0 1
m0
|
m1
|
x 0
|
x’y’
|
x’y
| |
m2
|
m3
|
1
|
xy’
|
xy
|
b. Peta dengan tiga peubah
yz
00
|
01
|
11
|
10
| |||||||
m0
|
m1
|
m3
|
m2
|
x 0
|
x’y’z’
|
x’y’z
|
x’yz
|
x’yz’
| ||
m4
|
m5
|
m7
|
m6
|
1
|
xy’z’
|
xy’z
|
xyz
|
xyz’
|
Contoh. Diberikan tabel kebenaran, gambarkan Peta Karnaugh.
x
|
y
|
Z
|
f(x, y, z)
| ||
0
|
0
|
0
|
0
| ||
0
|
0
|
1
|
0
| ||
0
|
1
|
0
|
1
| ||
0
|
1
|
1
|
0
| ||
1
|
0
|
0
|
0
| ||
1
|
0
|
1
|
0
| ||
1
|
1
|
0
|
1
| ||
1
|
1
|
1
|
1
|
b. Peta dengan empat peubah
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Contoh. Diberikan tabel kebenaran, gambarkan Peta Karnaugh.
w
|
x
|
Y
|
z
|
f(w, x, y, z)
| ||
0
|
0
|
0
|
0
|
0
| ||
0
|
0
|
0
|
1
|
1
| ||
0
|
0
|
1
|
0
|
0
| ||
0
|
0
|
1
|
1
|
0
| ||
0
|
1
|
0
|
0
|
0
| ||
0
|
1
|
0
|
1
|
0
| ||
0
|
1
|
1
|
0
|
1
| ||
0
|
1
|
1
|
1
|
1
| ||
1
|
0
|
0
|
0
|
0
| ||
1
|
0
|
0
|
1
|
0
| ||
1
|
0
|
1
|
0
|
0
| ||
1
|
0
|
1
|
1
|
0
| ||
1
|
1
|
0
|
0
|
0
| ||
1
|
1
|
0
|
1
|
0
| ||
1
|
1
|
1
|
0
|
1
| ||
1
|
1
|
1
|
1
|
0
| ||
yz
00
|
01
|
11
|
10
| |
wx 00
|
0
|
1
|
0
|
1
|
01
|
0
|
0
|
1
|
1
|
11
|
0
|
0
|
0
|
1
|
10
|
0
|
0
|
0
|
0
|
Teknik Minimisasi Fungsi Boolean dengan Peta Karnaugh
1. Pasangan: dua buah 1 yang bertetangga
yz
00
|
01
|
11
|
10
| |
wx 00
|
0
|
0
|
0
|
0
|
01
|
0
|
0
|
0
|
0
|
11
|
0
|
0
|
1
|
1
|
10
|
0
|
0
|
0
|
0
|
Sebelum disederhanakan: f(w, x, y, z) = wxyz + wxyz’
Hasil Penyederhanaan: f(w, x, y, z) = wxy
Bukti secara aljabar:
f(w, x, y, z) = wxyz + wxyz’
= wxy(z + z’)
= wxy(1)
= wxy
2. Kuad: empat buah 1 yang bertetangga
Sebelum disederhanakan: f(w, x, y, z) = wxy’z’ + wxy’z + wxyz + wxyz’
Hasil penyederhanaan: f(w, x, y, z) = wx
Bukti secara aljabar:
f(w, x, y, z) = wxy’ + wxy
= wx(z’ + z)
= wx
Sebelum disederhanakan: f(w, x, y, z) = wxy’z’ + wxy’z + wx’y’z’ + wx’y’z
Hasil penyederhanaan: f(w, x, y, z) = wy’
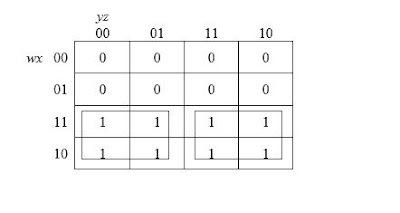
3. Oktet: delapan buah 1 yang bertetangga
Sebelum disederhanakan: f(a, b, c, d) = wxy’z’ + wxy’z + wxyz + wxyz’ +
wx’y’z’ + wx’y’z + wx’yz + wx’yz’
Hasil penyederhanaan: f(w, x, y, z) = w
Bukti secara aljabar:
f(w, x, y, z) = wy’ + wy
= w(y’ + y)
= w
Contoh 5.11. Sederhanakan fungsi Boolean f(x, y, z) = x’yz + xy’z’ + xyz + xyz’.
Jawab:
Peta Karnaugh untuk fungsi tersebut adalah:
Hasil penyederhanaan: f(x, y, z) = yz + xz’
Contoh 5.12. Andaikan suatu tabel kebenaran telah diterjemahkan ke dalam Peta Karnaugh. Sederhanakan fungsi Boolean yang bersesuaian sesederhana mungkin.
Jawab: (lihat Peta Karnaugh) f(w, x, y, z) = wy’ + yz’ + w’x’z
Contoh 5.13. Minimisasi fungsi Boolean yang bersesuaian dengan Peta Karnaugh di bawah ini.
Jawab: (lihat Peta Karnaugh) f(w, x, y, z) = w + xy’z
Jika penyelesaian Contoh 5.13 adalah seperti di bawah ini:
maka fungsi Boolean hasil penyederhanaan adalah
f(w, x, y, z) = w + w’xy’z (jumlah literal = 5)
yang ternyata masih belum sederhana dibandingkan f(w, x, y, z) = w + xy’z (jumlah literal = 4).
Contoh soal (Penggulungan/rolling) Sederhanakan fungsi Boolean yang bersesuaian dengan Peta Karnaugh di bawah ini.
Jawab: f(w, x, y, z) = xy’z’ + xyz’ ==> belum sederhana
Penyelesaian yang lebih minimal:
f(w, x, y, z) = xz’ bentuk lebih sederhana



















Komentar
Posting Komentar