INDUKSI MATEMATIKA DISKRIT

  INDUKSI MATEMATIKA

induksi matematika merupakan salah satu cara pembuktian rumus atau pernyataan matematika, atau lebih tepatnya metode pembuktian terhadap suatu pernyataan apakah pernyataan tersebut berlaku untuk setiap kasus. Supaya kebayang, sebaiknya kita langsung ke contoh kasus deh. Kasus yang seperti apa sih yang bisa diselesaikan dengan Induksi Matematika? Kita masuk ke contoh yang sederhana aja deh ya. Misalkan gue punya deret bilangan seperti di bawah ini.

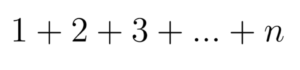
Untuk nilai n tertentu, kita bisa mencari jumlah dari deret bilangan di atas. Sebagai contoh, untuk n=2, kita mendapatkan hasil demikian:

Ternyata untuk n=2, kita mendapatkan bahwa jumlah deretnya adalah 3.
Bagaimana dengan n=5? Gampang, tinggal kita hitung aja lagi begini:

Jumlahnya adalah 15. Kalau untuk n=8 gimana? Sama aja caranya:

Kita dapatkan bahwa untuk n=8, jumlah deret tersebut adalah 40.
Kemudian kita mendapatkan informasi bahwa ternyata untuk menghitung jumlah deret tersebut untuk n bilangan asli berapapun, SUDAH ADA RUMUSNYA. Jadi, kita nggak perlu repot-repot menjumlahkan satu per satu seperti di atas, tapi tinggal kita masukkan saja nilai n ke dalam rumus tersebut. Bagaimana tuh rumusnya? Untuk deret di atas, rumus jumlahnya adalah demikian:

 

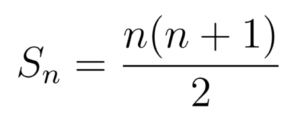
Gimana Buktiinnya?

Yup. Gimana buktiinnya kalo rumus Sn di atas udah bener?
Nah, sebelum masuk ke pembuktian dengan Induksi Matematika, coba deh kita tes dulu apakah nilai Sn itu benar untuk nilai-nilai n yang sebelumnya udah kita hitung. Kita mulai dari n=2.

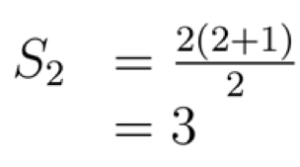
Wah, ternyata benar nih. Hasilnya sama untuk n=2. Sekarang coba kita tes untuk n=5.

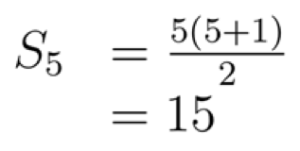
Hasilnya sama lagi nih. Untuk n=8 gimana?

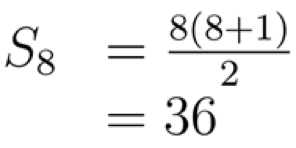
Bener lagi! Okay, kalau gitu, bisa kita simpulkan bahwa rumus Sn ini benar lah ya? Eit, tunggu dulu. Kita baru menguji untuk tiga nilai n. Dalam matematika, kita tidak bisa melakukan generalisasi seperti itu. Untuk bisa membuktikan bahwa rumus Sn ini benar untuk semua kasus, kita harus benar-benar bisa membuktikan bahwa rumus Sn ini benar untuk SEMUA nilai n bilangan asli.
Wah, kalau mau membuktikan untuk semua nilai n, kapan selesainya? Kan ada banyak banget yang harus dicoba. Nilai n=9, nilai n=10, nilai n=100, nilai n=84349384, dan seterusnya. Ada tak hingga nilai n yang harus kita coba. Nggak mungkin bisa kita cobain semuanya.
Nah, itulah sebabnya kita perlu membuktikannya dengan menggunakan Induksi Matematika.

Konsep Dasar Induksi Matematika

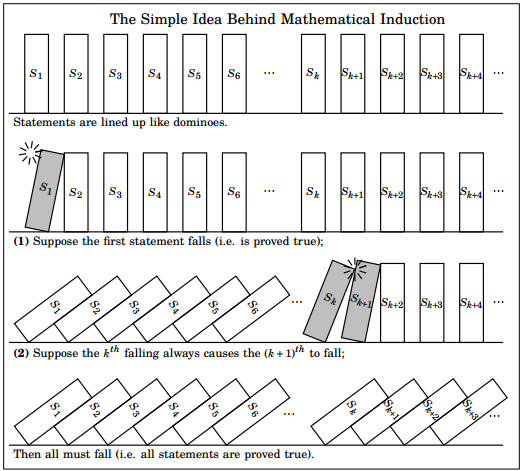
Dengan menggunakan Induksi Matematika, kita bisa membuktikan rumus Sn di atas tanpa perlu menghitung satu per satu nilai Sn seperti di atas. Caranya simple banget. Kita cuma butuh melakukan dua langkah berikut ini:

1. Buktikan bahwa rumus tersebut benar untuk nilai n dasar (pada contoh di atas, buktikan untuk n=1).
2. Buktikan bahwa jika rumus tersebut benar untuk n=k, maka rumus tersebut juga benar untuk n=k+1.

   Pembuktian dengan Induksi Matematika

   Nah, di atas kita udah mempelajari konsep dasar dari Induksi Matematika ya. Sekarang, kita lanjut ke proses pembuktian dengan Induksi Matematikanya. Kita balik lagi ke contoh di atas, yaitu deret ini:
   
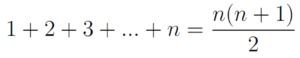
   Deret ini memiliki Un = n dan Sn = n(n+1)/2. Coba kita buktikan dengan Induksi Matematika bahwa rumus Sn ini benar.
   LANGKAH 1: Buktikan bahwa Sn benar untuk n=1.
   Bagian ini gampang nih. Kita tahu bahwa untuk n=1, jumlahnya harus sama dengan 1. Berarti kalau S1 itu sama dengan 1, langkah satu beres.
   
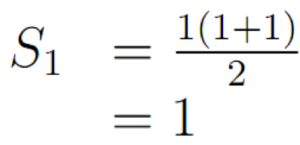
   Sip. Rumus Sn ini lolos pada langkah satu. Berikutnya, langkah 2.
   LANGKAH 2: Buktikan bahwa jika Sn benar untuk n=k, maka Sn juga benar untuk n=k+1.
   Nah, untuk bagian ini, teknik membuktikannya adalah dengan membuktikan bahwa persamaan di bawah ini benar.
   
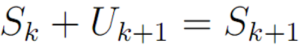
   Kalau persamaan di atas benar, itu sama saja dengan membuktikan bahwa jika Sk benar, maka Sk+1 juga benar.
   So, kalau kita masukkan n=k dan n=k+1 pada rumus Sn, maka kita akan mendapatkan:
   
   Kalau begitu, tinggal kita buktikan saja dengan cara demikian:
   
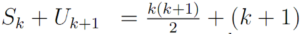
   Bagian (k+1)-nya kita kotakin kemudian kita keluarkan (hukum distributif)
   
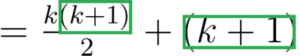
   Sehingga kita dapatkan:
   
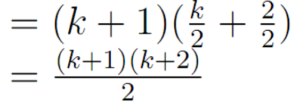
   Ternyata hasilnya sama peris dengan Sk+1 yang kita hitung pada tabel di atas. Berarti kita dapat simpulkan bahwa persamaan berikut ini:
   
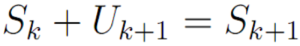
   Adalah benar!
   Karena Sn terbukti benar pada langkah 1 dan juga terbukti benar pada langkah 2, maka kita bisa simpulkan bahwa rumus Sn benar untuk semua n bilangan asli! Q. E. D.*